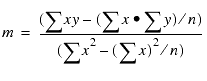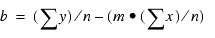Calculating Trends and Predicting Values With FORECAST
You can calculate trends in numeric data and predict
values beyond the range of those stored in the data source by using
the FORECAST feature. FORECAST can be used in a report
or graph request.
The calculations you can make to identify
trends and forecast values are:
-
Simple moving average (MOVAVE). Calculates
a series of arithmetic means using a specified number of values
from a field. For details, see Using a Simple Moving Average.
-
Exponential moving average. Calculates
a weighted average between the previously calculated value of the
average and the next data point. There are three methods for using
an exponential moving average:
-
Single exponential smoothing (EXPAVE). Calculates
an average that allows you to choose weights to apply to newer and
older values. For details, see Using Single Exponential Smoothing.
-
Double exponential smoothing (DOUBLEXP). Accounts
for the tendency of data to either increase or decrease over time
without repeating. For details, see Using Double Exponential Smoothing.
-
Triple exponential smoothing (SEASONAL). Accounts
for the tendency of data to repeat itself in intervals over time.
For details, see Using Triple Exponential Smoothing.
-
Linear regression analysis (REGRESS). Derives
the coefficients of a straight line that best fits the data points and
uses this linear equation to estimate values. For details, see Usage Notes for Creating Virtual Fields.
When predicting values in addition to calculating trends, FORECAST continues
the same calculations beyond the data points by using the generated
trend values as new data points. For the linear regression technique,
the calculated regression equation is used to derive trend and predicted
values.
FORECAST performs
the calculations based on the data provided, but decisions about
their use and reliability are the responsibility of the user. Therefore, FORECAST predictions
are not always reliable, and many factors determine how accurate
a prediction will be.
x
You invoke FORECAST processing
by including FORECAST in a RECAP command. In this command,
you specify the parameters needed for generating estimated values,
including the field to use in the calculations, the type of calculation
to use, and the number of predictions to generate. The RECAP field
that contains the result of FORECAST can be a new field (non-recursive)
or the same field used in the FORECAST calculations (recursive):
- In a recursive FORECAST,
the RECAP field
that contains the results is also the field used to generate the FORECAST
calculations. In this case, the original field is not printed even
if it was referenced in the display command, and the RECAP column
contains the original field values followed by the number of predicted
values specified in the FORECAST syntax. No trend values
display in the report. However, the original column is stored in
an output file unless you set HOLDLIST to PRINTONLY.
- In a non-recursive
FORECAST,
a new field contains the results of FORECAST calculations. The new field
is displayed in the report along with the original field when it
is referenced in the display command. The new field contains trend
values and forecast values when specified.
FORECAST operates
on the last ACROSS field in the request. If
the request does not contain an ACROSS field, it operates on the
last BY field.
The FORECAST calculations start over
when the highest-level sort field changes its value. In a request
with multiple display commands, FORECAST operates on the last ACROSS field
(or if there are no ACROSS fields, the last BY field) of
the last display command. When using
an ACROSS field with FORECAST, the display command must be SUM or
COUNT.
Note: Although you pass parameters to FORECAST using
an argument list in parentheses, FORECAST is not a function. It can
coexist with a function of the same name, as long as the function
is not specified in a RECAP command.
x
Syntax: How to Calculate Trends and Predict Values
MOVAVE calculation
ON sortfield RECAP result_field[/fmt] = FORECAST(infield, interval,
npredict, 'MOVAVE',npoint1);
EXPAVE calculation
ON sortfield RECAP result_field[/fmt] = FORECAST(infield, interval,
npredict, 'EXPAVE',npoint1);
DOUBLEXP calculation
ON sortfield RECAP fld1[/fmt] = FORECAST(infield,
interval, npredict, 'DOUBLEXP',npoint1, npoint2);
SEASONAL calculation
ON sortfield RECAP fld1[/fmt] = FORECAST(infield,
interval, npredict, 'SEASONAL', nperiod, npoint1, npoint2, npoint3);
REGRESS calculation
ON sortfield RECAP result_field[/fmt] = FORECAST(infield, interval,
npredict, 'REGRESS');
where:
- sortfield
- Is the last ACROSS field in the request. This field must be
in numeric or date format. If the request does not contain an ACROSS
field, FORECAST works on the last BY field.
- result_field
- Is the field containing the result of FORECAST. It can be a
new field, or the same as infield. This must be a numeric
field; either a real field, a virtual field, or a calculated field.
Note: The
word FORECAST and the opening parenthesis must be on the same line
as the syntax sortfield=.
- fmt
- Is the display format for result_field. The default format
is D12.2. If result_field was previously reformatted using
a DEFINE or COMPUTE command, the format specified in the RECAP command
is respected.
- infield
- Is any numeric field. It can be the same field as result_field,
or a different field. It cannot be a date-time field or a numeric
field with date display options.
- interval
- Is the increment to add to each sortfield value (after
the last data point) to create the next value. This must be a positive
integer. To sort in descending order, use the BY HIGHEST phrase.
The result of adding this number to the sortfield values
is converted to the same format as sortfield.
For date
fields, the minimal component in the format determines how the number is
interpreted. For example, if the format is YMD, MDY, or DMY, an
interval value of 2 is interpreted as meaning two days; if the format
is YM, the 2 is interpreted as meaning two months.
- npredict
- Is the number of predictions for FORECAST to calculate. It must
be an integer greater than or equal to zero. Zero indicates that
you do not want predictions, and is only supported with a non-recursive
FORECAST. For the SEASONAL method, npredict is the number of periods to
calculate. The number of points generated is:
nperiod * npredict
- nperiod
- For the SEASONAL method, is a positive whole number that specifies
the number of data points in a period.
- npoint1
- Is the number of values to average for the MOVAVE method. For
EXPAVE, DOUBLEXP, and SEASONAL, this number is used to calculate
the weights for each component in the average. This value must be
a positive whole number. The weight, k, is calculated by the following
formula:
k=2/(1+npoint1)
- npoint2
- For DOUBLEXP and SEASONAL, this positive whole number is used
to calculate the weights for each term in the trend. The weight,
g, is calculated by the following formula:
g=2/(1+npoint2)
- npoint3
- For SEASONAL, this positive whole number is used to calculate
the weights for each term in the seasonal adjustment. The weight,
p, is calculated by the following formula:
p=2/(1+npoint3)
x
Reference: Usage Notes for FORECAST
- The sort field used
for FORECAST must be in a numeric or
date format.
- When using simple
moving average and exponential moving average methods, data values
should be spaced evenly in order to get meaningful results.
- When using a RECAP command with FORECAST,
the command can
contain only the FORECAST syntax. FORECAST does
not recognize any syntax after the closing semicolon (;). To specify
options such as AS or IN:
- In a non-recursive FORECAST request, use
an empty COMPUTE command prior to the RECAP.
- In a recursive FORECAST request,
specify the options when the field is first referenced in the report
request.
- The use of column
notation is not supported in a request that includes FORECAST.
The process of generating the FORECAST values creates extra columns
that are not printed in the report output. The number and placement
of these additional columns varies depending on the specific request.
- A request can contain
up to seven non-FORECAST
RECAP
commands and
up to seven additional FORECAST RECAP
commands.
- The left side of
a RECAP command used for FORECAST supports
the CURR attribute for creating a currency-denominated field.
- Recursive and non-recursive
REGRESS are not supported in the same request when the display command
is SUM, ADD, or WRITE.
- Missing values are
not supported with REGRESS.
- If you use the ESTRECORDS
parameter to enable the external sort to estimate better the amount
of sort work space needed, you must take into account that FORECAST with
predictions creates additional records in the output.
- In a styled report,
you can assign specific attributes to values predicted by FORECAST with
the StyleSheet attribute WHEN=FORECAST. For example, to make the
predicted values display with the color red, use the following syntax
in the TABLE request:
ON TABLE SET STYLE *TYPE=DATA,COLUMN=MYFORECASTSORTFIELD,WHEN=FORECAST,COLOR=RED,
$
ENDSTYLE
x
Reference:
FORECAST Limits
The following
are not supported with a RECAP command that uses FORECAST:
- BY TOTAL command.
- MORE, MATCH, FOR,
and OVER phrases.
- SUMMARIZE and RECOMPUTE
are not supported for the same sort field used for FORECAST.
- MISSING attribute.
xUsing a Simple Moving Average
A simple moving average is a series of arithmetic means
calculated with a specified number of values from a field. Each
new mean in the series is calculated by dropping the first value
used in the prior calculation, and adding the next data value to
the calculation.
Simple moving averages are sometimes used to analyze trends in
stock prices over time. In this scenario, the average is calculated
using a specified number of periods of stock prices. A disadvantage
to this indicator is that because it drops the oldest values from
the calculation as it moves on, it loses its memory over time. Also,
mean values are distorted by extreme highs and lows, since this
method gives equal weight to each point.
Predicted values beyond the range of the data values are calculated
using a moving average that treats the calculated trend values as
new data points.
The first complete moving average occurs at the nth data
point because the calculation requires n values. This is
called the lag. The moving average values for the lag rows are calculated
as follows: the first value in the moving average column is equal
to the first data value, the second value in the moving average
column is the average of the first two data values, and so on until
the nth row, at which point there are enough values to
calculate the moving average with the number of values specified.
Example: Calculating a New Simple Moving Average Column
This request defines an integer value
named PERIOD to use as the independent variable for the moving average.
It predicts three periods of values beyond the range of the retrieved
data.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM UNITS DOLLARS
BY CATEGORY BY PERIOD
WHERE SYEAR EQ 97 AND CATEGORY NE 'Gifts'
ON PERIOD RECAP MOVAVE/D10.1= FORECAST(DOLLARS,1,3,'MOVAVE',3);
END
The output is:
In
the report, the number of values to use in the average is 3 and
there are no UNITS or DOLLARS values for the generated PERIOD values.
Each average (MOVAVE value) is computed
using DOLLARS values where they exist. The calculation of the moving
average begins in the following way:
- The first MOVAVE
value (801,123.0) is equal to the first DOLLARS value.
- The second MOVAVE
value (741,731.5) is the mean of DOLLARS values one and two: (801,123
+ 682,340) /2.
- The third MOVAVE
value (749,513.7) is the mean of DOLLARS values one through three:
(801,123 + 682,340 + 765,078) / 3.
- The fourth MOVAVE
value (712,897.3) is the mean of DOLLARS values two through four:
(682,340 + 765,078 + 691,274) /3.
For predicted values
beyond the supplied values, the calculated MOVAVE values are used
as new data points to continue the moving average. The predicted
MOVAVE values (starting with 694,975.6 for PERIOD 13) are calculated
using the previous MOVAVE values as new data points. For example,
the first predicted value (694,975.6) is the average of the data
points from periods 11 and 12 (620,264 and 762,328) and the moving
average for period 12 (702,334.7). The calculation is: 694,975 =
(620,264 + 762,328 + 702,334.7)/3.
Example: Using an Existing Field as a Simple Moving Average Column
This request defines an integer value
named PERIOD to use as the independent variable for the moving average.
It predicts three periods of values beyond the range of the retrieved
data. It uses the same name for the RECAP field as the first argument
in the FORECAST parameter list. The trend values do not display
in the report. The actual data values for DOLLARS are followed by
the predicted values in the report column.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM UNITS DOLLARS
BY CATEGORY BY PERIOD
WHERE SYEAR EQ 97 AND CATEGORY NE 'Gifts'
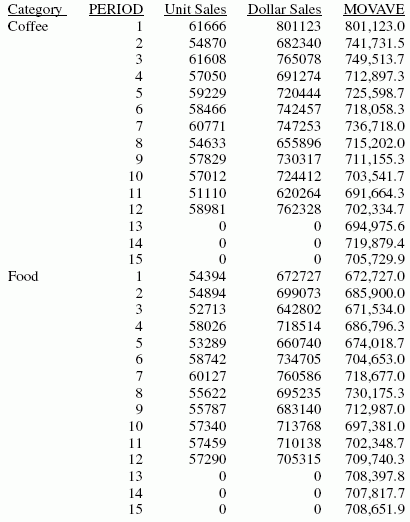
ON PERIOD RECAP DOLLARS/D10.1 = FORECAST(DOLLARS,1,3,'MOVAVE',3);
END
The output is:
xUsing Single Exponential Smoothing
The single exponential smoothing
method calculates an average that allows you to choose weights to
apply to newer and older values.
The following formula determines the
weight given to the newest value.
k = 2/(1+n)
where:
- k
- Is the newest value.
- n
- Is an integer greater than one. Increasing n increases
the weight assigned to the earlier observations (or data instances),
as compared to the later ones.
The next calculation of the exponential
moving average (EMA) value is derived by the following formula:
EMA = (EMA * (1-k)) + (datavalue * k)
This means that the newest value from the data source is multiplied
by the factor k and the current moving average is multiplied
by the factor (1-k). These quantities are then summed to
generate the new EMA.
Note: When the data values are exhausted, the last data
value in the sort group is used as the next data value.
Example: Calculating a Single Exponential Smoothing Column
The following defines an integer value
named PERIOD to use as the independent variable for the moving average.
It predicts three periods of values beyond the range of retrieved
data.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM UNITS DOLLARS
BY CATEGORY BY PERIOD
WHERE SYEAR EQ 97 AND CATEGORY NE 'Gifts'
ON PERIOD RECAP EXPAVE/D10.1= FORECAST(DOLLARS,1,3,'EXPAVE',3);
END
The output is:
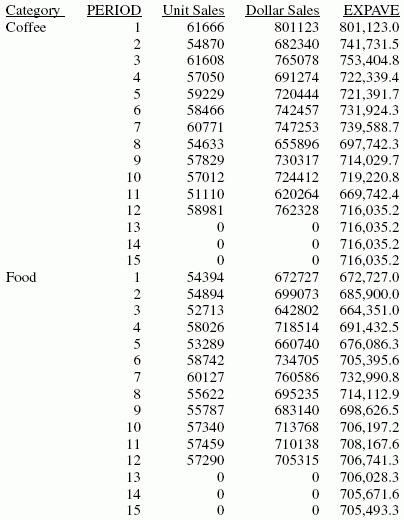
In
the report, three predicted values of EXPAVE are calculated within
each value of CATEGORY. For values outside the range of the data,
new PERIOD values are generated by adding the interval value (1)
to the prior PERIOD value.
Each average
(EXPAVE value) is computed using DOLLARS values where they exist.
The calculation of the moving average begins in the following way:
- The first EXPAVE
value (801,123.0) is the same as the first DOLLARS value.
- The second EXPAVE
value (741,731.5) is calculated as follows. Note that because of
rounding and the number of decimal places used, the value derived
in this sample calculation varies slightly from the one displayed
in the report output:
n=3 (number used to calculate weights)
k = 2/(1+n) = 2/4 = 0.5
EXPAVE = (EXPAVE*(1-k))+(new-DOLLARS*k) = (801123*0.5) + (682340*0.50) = 400561.5 + 341170 = 741731.5
- The third EXPAVE
value (753,404.8) is calculated as follows:
EXPAVE = (EXPAVE*(1-k))+(new-DOLLARS*k) = (741731.5*0.5)+(765078*0.50) = 370865.75 + 382539 = 753404.75
For predicted values beyond those supplied,
the last EXPAVE value is used as the new data point in the exponential
smoothing calculation. The predicted EXPAVE values (starting with
706,741.6) are calculated using the previous average and the new
data point. Because the previous average is also used as the new
data point, the predicted values are always equal to the last trend
value. For example, the previous average for period 13 is 706,741.6, and
this is also used as the next data point. Therefore, the average
is calculated as follows: (706,741.6 * 0.5) + (706,741.6 * 0.5)
= 706,741.6
EXPAVE = (EXPAVE * (1-k)) + (new-DOLLARS * k) = (706741.6*0.5) +
(706741.6*0.50) = 353370.8 + 353370.8 = 706741.6
xUsing Double Exponential Smoothing
Double exponential smoothing produces an exponential
moving average that takes into account the tendency of data to either
increase or decrease over time without repeating. This is accomplished
by using two equations with two constants.
These two equations are solved to derive the smoothed average.
The first smoothed average is set to the first data value. The first
trend component is set to zero. For choosing the two constants,
the best results are usually obtained by minimizing the mean-squared error
(MSE) between the data values and the calculated averages. You may
need to use nonlinear optimization techniques to find the optimal
constants.
The equation used for forecasting beyond
the data points with double exponential smoothing is
forecast(t+m) = DOUBLEXP(t) + m * b(t)
where:
- m
- Is the number of time periods ahead for the forecast.
Example: Calculating a Double Exponential Smoothing Column
The following defines an integer value
named PERIOD to use as the independent variable for the moving average.
The double exponential smoothing method estimates the trend in the
data points better than the single smoothing method:
SET HISTOGRAM = OFF
TABLE FILE CENTSTMT
SUM ACTUAL_YTD
BY PERIOD
ON PERIOD RECAP EXP/D15.1 = FORECAST(ACTUAL_YTD,1,0,'EXPAVE',3);
ON PERIOD RECAP DOUBLEXP/D15.1 = FORECAST(ACTUAL_YTD,1,0,
'DOUBLEXP',3,3);
WHERE GL_ACCOUNT LIKE '3%%%'
ENDThe output is:
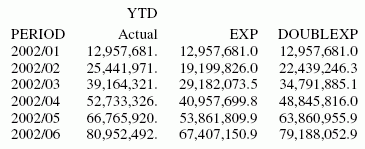
xUsing Triple Exponential Smoothing
Triple exponential smoothing produces an exponential
moving average that takes into account the tendency of data to repeat
itself in intervals over time. For example, sales data that is growing
and in which 25% of sales always occur during December contains both
trend and seasonality. Triple exponential smoothing takes both the
trend and seasonality into account by using three equations with
three constants.
For triple exponential smoothing you,
need to know the number of data points in each time period (designated
as L in the following equations). To account for the seasonality,
a seasonal index is calculated. The data is divided by the prior
season index and then used in calculating the smoothed average.
- The first equation
accounts for the current time period, and is a weighted average
of the current data value divided by the seasonal factor and the
prior average adjusted for the trend for the previous period. The
weight constant is k:
SEASONAL(t) = k * (datavalue(t)/I(t-L)) + (1-k) * (SEASONAL(t-1) + b(t-1))
- The second equation
is the calculated trend value, and is a weighted average of the
difference between the current and previous average and the trend
for the previous time period. b(t) represents the average
trend. The weight constant is g:
b(t) = g * (SEASONAL(t)-SEASONAL(t-1)) + (1-g) * (b(t-1))
- The third equation
is the calculated seasonal index, and is a weighted average of the
current data value divided by the current average and the seasonal
index for the previous season. I(t) represents the average
seasonal coefficient. The weight constant is p:
I(t) = p * (datavalue(t)/SEASONAL(t)) + (1 - p) * I(t-L)
These equations are solved to derive the triple smoothed average.
The first smoothed average is set to the first data value. Initial
values for the seasonality factors are calculated based on the maximum
number of full periods of data in the data source, while the initial trend
is calculated based on two periods of data. These values are calculated
with the following steps:
- The initial trend
factor is calculated by the following formula:
b(0) = (1/L) ((y(L+1)-y(1))/L + (y(L+2)-y(2))/L + ... + (y(2L) -
y(L))/L )
- The calculation of
the initial seasonality factor is based on the average of the data values
within each period, A(j) (1<=j<=N):
A(j) = ( y((j-1)L+1) + y((j-1)L+2) + ... + y(jL) ) / L
- Then, the initial
periodicity factor is given by the following formula, where N is
the number of full periods available in the data, L is the number
of points per period and n is a point within the period (1<=
n <= L):
I(n) = ( y(n)/A(1) + y(L+n)/A(2) + ... + y((N-1)L+n)/A(N) ) / N
The three constants must be chosen carefully. The best results
are usually obtained by choosing the constants to minimize the mean-squared
error (MSE) between the data values and the calculated averages.
Varying the values of npoint1 and npoint2 affect the results, and
some values may produce a better approximation. To search for a
better approximation, you may want to find values that minimize
the MSE.
The equation used to forecast beyond
the last data point with triple exponential smoothing is:
forecast(t+m) = (SEASONAL(t) + m * b(t)) / I(t-L+MOD(m/L))
where:
- m
- Is the number of periods ahead for the forecast.
Example: Calculating a Triple Exponential Smoothing Column
In the following, the data has seasonality
but no trend. Therefore, npoint2 is set high (1000) to make
the trend factor negligible in the calculation:
SET HISTOGRAM = OFF
TABLE FILE VIDEOTRK
SUM TRANSTOT
BY TRANSDATE
ON TRANSDATE RECAP SEASONAL/D10.1 = FORECAST(TRANSTOT,1,3,'SEASONAL',
3,3,1000,1);
WHERE TRANSDATE NE '19910617'
END
In the output, npredict is
3. Therefore, three periods (nine points, nperiod * npredict)
are generated.
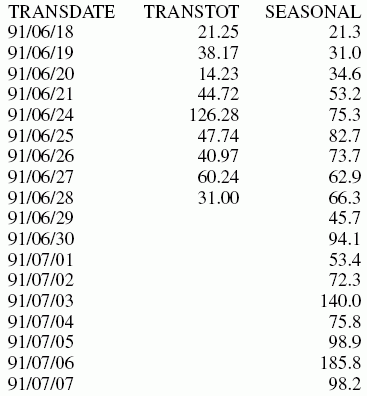
xUsing a Linear Regression Equation
The Linear Regression Equation
estimates values by assuming that the dependent variable (the new
calculated values) and the independent variable (the sort field values)
are related by a function that represents a straight line:
y = mx + b
where:
- y
- Is the dependent variable.
- x
- Is the independent variable.
- m
- Is the slope of the line.
- b
- Is the y-intercept.
REGRESS uses a technique called Ordinary Least Squares to calculate
values for m and b that minimize the sum of the squared
differences between the data and the resulting line.
The following formulas show how m and b are
calculated.
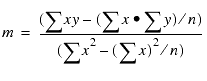
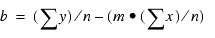
where:
- n
- Is the number of data points.
- y
- Is the data values (dependent variables).
- x
- Is the sort field values (independent variables).
Trend values, as well as predicted values, are calculated using
the regression line equation.
Example: Calculating a New Linear Regression Field
TABLE FILE CAR
PRINT MPG
BY DEALER_COST
WHERE MPG NE 0.0
ON DEALER_COST RECAP FORMPG=FORECAST(MPG,1000,3,'REGRESS');
END
The output is:
DEALER_COST MPG FORMPG
2,886 27 25.51
4,292 25 23.65
4,631 21 23.20
4,915 21 22.82
5,063 23 22.63
5,660 21 21.83
21 21.83
5,800 24 21.65
6,000 24 21.38
7,427 16 19.49
8,300 18 18.33
8,400 18 18.20
10,000 18 16.08
11,000 18 14.75
11,194 9 14.50
14,940 11 9.53
15,940 0 8.21
16,940 0 6.88
17,940 0 5.55Note:
- Three predicted values
of FORMPG are calculated. For values outside the range of the data,
new DEALER_COST values are generated by adding the interval value (1,000)
to the prior DEALER_COST value.
- There are no MPG
values for the generated DEALER_COST values.
- Each FORMPG value
is computed using a regression line, calculated using all of the actual
data values for MPG.
DEALER_COST is the independent variable
(x) and MPG is the dependent variable (y). The equation is used
to calculate MPGFORECAST trend and predicted values.
In this case, the equation is approximately
as follows:
FORMPG = (-0.001323 * DEALER_COST) + 29.32
The predicted values are (the values
are not exactly as calculated by FORECAST because of rounding, but
they show the calculation process).
DEALER_COST | Calculation | FORMPG |
|---|
15,940 | (-0.001323 * 15,940)
+ 29.32 | 8.23 |
16,940 | (-0.001323 * 16,940) + 29.32 | 6.91 |
17,940 | (-0.001323 * 17,940) + 29.32 | 5.59 |
x
FORECAST Reporting Techniques
You can use FORECAST multiple times in one request.
However, all FORECAST requests must specify the
same sort field, interval, and number of predictions. The only things
that can change are the RECAP field, method, field used to
calculate the FORECAST values, and number of points
to average. If you change any of the other parameters, the new parameters
are ignored.
If you want to move a FORECAST column in the report output,
use an empty COMPUTE command for the FORECAST field
as a placeholder. The data type (I, F, P, D) must be the same in
the COMPUTE command and the RECAP command.
To make the report output easier to interpret, you can create
a field that indicates whether the FORECAST value in each row is a predicted value.
To do this, define a virtual field whose value is a constant other
than zero. Rows in the report output that represent actual records
in the data source will appear with this constant. Rows that represent
predicted values will display zero. You can also propagate this
field to a HOLD file.
Example: Generating Multiple FORECAST Columns in a Request
This example calculates moving averages
and exponential averages for both the DOLLARS and BUDDOLLARS fields
in the GGSALES data source. The sort field, interval, and number
of predictions are the same for all of the calculations.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM DOLLARS AS 'DOLLARS' BUDDOLLARS AS 'BUDGET'
BY CATEGORY NOPRINT BY PERIOD AS 'PER'
WHERE SYEAR EQ 97 AND CATEGORY EQ 'Coffee'
ON PERIOD RECAP DOLMOVAVE/D10.1= FORECAST(DOLLARS,1,0,'MOVAVE',3);
ON PERIOD RECAP DOLEXPAVE/D10.1= FORECAST(DOLLARS,1,0,'EXPAVE',4);
ON PERIOD RECAP BUDMOVAVE/D10.1 = FORECAST(BUDDOLLARS,1,0,'MOVAVE',3);
ON PERIOD RECAP BUDEXPAVE/D10.1 = FORECAST(BUDDOLLARS,1,0,'EXPAVE',4);
END
The output is shown in
the following image.
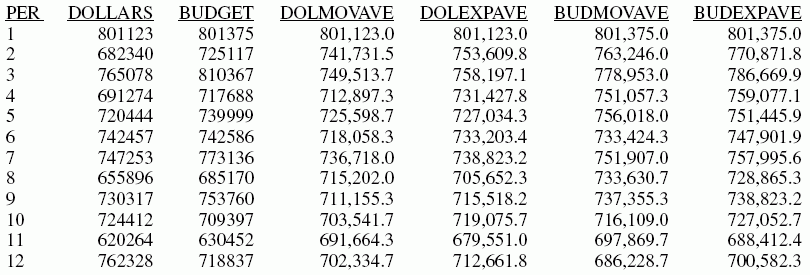
Example: Moving the FORECAST Column
The following example places the DOLLARS
field after the MOVAVE field by using an empty COMPUTE command as
a placeholder for the MOVAVE field. Both the COMPUTE command and
the RECAP command specify formats for MOVAVE (of the same data type), but
the format of the RECAP command takes precedence.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM UNITS
COMPUTE MOVAVE/D10.2 = ;
DOLLARS
BY CATEGORY BY PERIOD
WHERE SYEAR EQ 97 AND CATEGORY EQ 'Coffee'
ON PERIOD RECAP MOVAVE/D10.1= FORECAST(DOLLARS,1,3,'MOVAVE',3);
END
The output is shown in
the following image.
Category PERIOD Unit
Sales MOVAVE Dollar
SalesCoffee 1 61666 801,123.0 801123
2 54870 741,731.5 682340
3 61608 749,513.7 765078
4 57050 712,897.3 691274
5 59229 725,598.7 720444
6 58466 718,058.3 742457
7 60771 736,718.0 747253
8 54633 715,202.0 655896
9 57829 711,155.3 730317
10 57012 703,541.7 724412
11 51110 691,664.3 620264
12 58981 702,334.7 762328
13 0 694,975.6 0
14 0 719,879.4 0
15 0 705,729.9 0
Example: Distinguishing Data Rows From Predicted Rows
In the following example, the DATA_ROW
virtual field has the value 1 for each row in the data source. It
has the value zero for the predicted rows. The PREDICT field is
calculated as YES for predicted rows, and NO for rows containing
data.
DEFINE FILE CAR
DATA_ROW/I1 = 1;
END
TABLE FILE CAR
PRINT DATA_ROW
COMPUTE PREDICT/A3 = IF DATA_ROW EQ 1 THEN 'NO' ELSE 'YES' ;
MPG
BY DEALER_COST
WHERE MPG GE 20
ON DEALER_COST RECAP FORMPG/D12.2=FORECAST(MPG,1000,3,'REGRESS');
ON DEALER_COST RECAP MPG =FORECAST(MPG,1000,3,'REGRESS');
END
The output is:
DEALER_COST DATA_ROW PREDICT MPG FORMPG
2,886 1 NO 27.00 25.65
4,292 1 NO 25.00 23.91
4,631 1 NO 21.00 23.49
4,915 1 NO 21.00 23.14
5,063 1 NO 23.00 22.95
5,660 1 NO 21.00 22.21
1 NO 21.00 22.21
5,800 1 NO 24.20 22.04
6,000 1 NO 24.20 21.79
7,000 0 YES 20.56 20.56
8,000 0 YES 19.32 19.32
9,000 0 YES 18.08 18.08